Imaginad un trilero que os propone el siguiente juego de azar:
- Has de tirar una moneda al aire, si sale cara ganas 2 euros, si sale cruz, nada.
Un ejemplo más complicado:
- Has de tirar una moneda al aire, si sale cara recibes un euro y puedes seguir tirando, si sale cruz se acabó.
(Si no tienes ganas de leer cosas demasiado matemáticas salta hasta que veas el próximo aviso en rojo)
La probabilidad de ganar un euro (perder a la segunda) es 1/2·1/2, la de ganar dos euros es 1/2·1/2·1/2 y en general la probabilidad de ganar n euros es 1/2^(n+1).
La esperanza de este juego sería multiplicar cada posible ganancia por su probabilidad y sumarlo todo, así:
1·(1/2)^2 + 2·(1/2)^3 + 3·(1/2)^4 + 4·(1/2)^5 + 5·(1/2)^6+...
Matemáticamente se expresa:
Esto es la suma de los infinitos elementos de una serie aritmético-geométrica, llamémosla S. Para poder calcular esa suma se sigue un procedimiento muy astuto, bastante fácil de seguir y a algunos hasta os sonará de la carrera. Se trata de considerar esa misma serie multiplicada por 1/2 para poder así desplazar todos los elementos una posición.
Queremos restar S menos S/2 para simplificar la serie pero primero hay que manipular la expresión original de S así:
 Ahora sí hacemos una ecuación nueva mediante S-S/2 ya que así se anulan muchos términos y me queda solo una serie geométrica que sí tiene solución,
Ahora sí hacemos una ecuación nueva mediante S-S/2 ya que así se anulan muchos términos y me queda solo una serie geométrica que sí tiene solución,Aplicando la solución general de una serie geométrica (esto os debe sonar):
Sustituimos en la ecuación "nueva" que habíamos preparado y obtenemos:
Así que la esperanza en este caso es un euro, esa sería la ganancia promedio y por tanto el precio justo para jugar.
(Vale, nos reunimos aquí todos y seguimos con la visita)
Y ahora la madre del cordero, esto es a lo que veníamos, un caso similar pero paradójico:
Te proponen este juego:
- Igual que antes vas tirando mientras saques cara, si sales cruz paras.
- La primera cara obtienes un euro y a partir de ahí el doble cada vez.
Por tanto la esperanza es ganar infinito. ¿Cuanto habría que pagar por jugar? Da igual lo alto que fuera el precio, siempre sería ventajoso para el jugador. Pero eso no es muy intuitivo, está claro que si me piden 1000€ por jugar sería muy raro que los recupere, ¡tendría que sacar diez caras seguidas! Pero las matemáticas son correctas. ¿Cómo hay que interpretarlo? Si jugar costase un euro... ¿valdría la pena jugar? ¿Cuantas veces hay que jugar para que empiece a valer la pena?
Voy a parar aquí para que aportéis vuestras opiniones y razonamientos sobre ésta última paradoja.

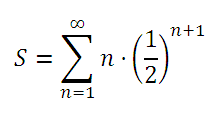






3 comentarios:
La probabilidad de que te salgan 5, 6, 7,... caras seguidas muy alta no debe ser. Por ejemplo, en el caso de 6 caras seguidas es 0.015. Dada mi gran suerte en el mundo del juego yo establecería que más de tres caras seguidas no me van a salir (p = 0.125, y ya me estoy lanzando a la piscina). La esperanza en este caso, obviando todos los demás resultados "buenos", es 3. Por lo tanto nunca pagaría más de tres euros por jugar. No creo que haya respondido bien, porqué en realidad no pagaría más de un euro.
Hombre eso que dices es muy a "ojímetro" pero es razonable. Tu ya estás en otro nivel intentando calcular el precio justo de una manera más humana.
Pero matemáticamente da infinito. ¿Quieres decir que los cálculos están mal? ¿O que no se puede equiparar la esperanza con el precio justo? Si jugases indefinidamente... ¿Poco a poco recuperarías dinero y acabarías ganando?
A mi me mosquea bastante.
Hombre, la esperanza, aunque matemáticamente correcta, solo tiene sentido si juegas infinitas veces. Si vas a jugar dos o tres veces, pues no, no?
Publicar un comentario